zeolites bokeh python 28 March 2017

Zeolite Framework Classification

Visualization of zeolite topologies classification using bokeh.

Introduction

Zeolites are fascinating materials with quite unique properties. They belong to what is often referred to as microporous materials which means that they contain pores that do not exceed 2 nm (20 Å). That is probably why they earned the name of molecular sieves since the pores match the sizes of small molecules allowing for size based discrimination. Initially they were a curiosity to mineralogists but since their discovery they opened a rich field of scientific activities and fallen under investigation by chemists, mathematicians, physicists, material scientists, biologists and probably some more.

From a structural point of view zeolites are built from tetrahedrons that have oxygen atoms at vertices and an atom of valency 4 at their centers. Those tetrahedrons connect with each other by sharing O atoms (vertices) and form intricate networks with repeatable patterns resulting in a variety of periodic crystalline materials.

Due to the number of possible ways that the network of interconnected tetrahedra can be arranged in space the number of resulting structures in overwhelmingly large, however not all of the possibilities will be energetically stable and even a smaller fraction is feasible to synthesize or find in nature.

As an illustration have a look below at the two possible frameworks that are labeled AFI and MTT. Both are composed of silicon (beige spheres) and oxygen atoms (red spheres) with AFI having 12 Si and 12 O atoms forming channels and MTT 10 Si and O atoms form the channels.

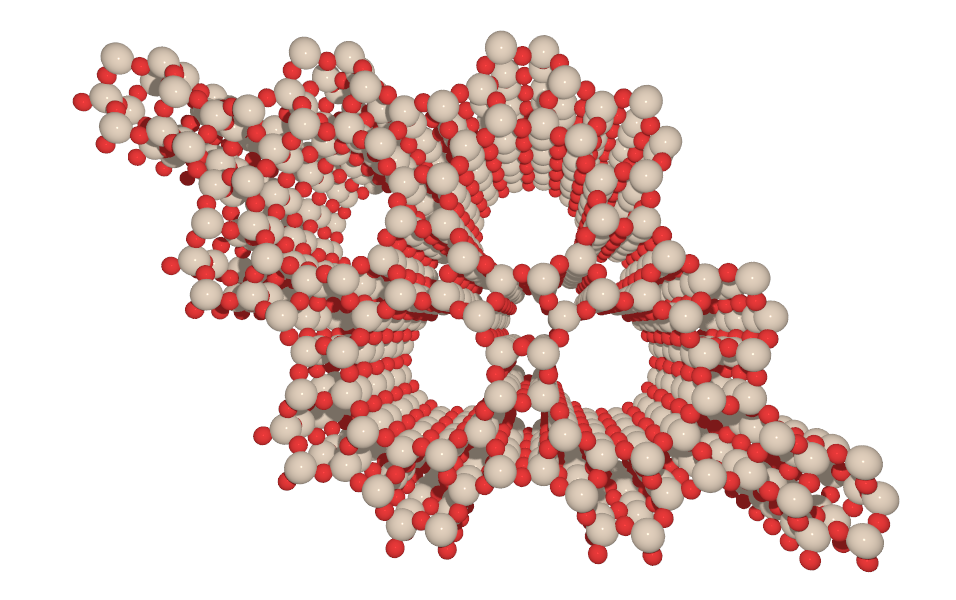
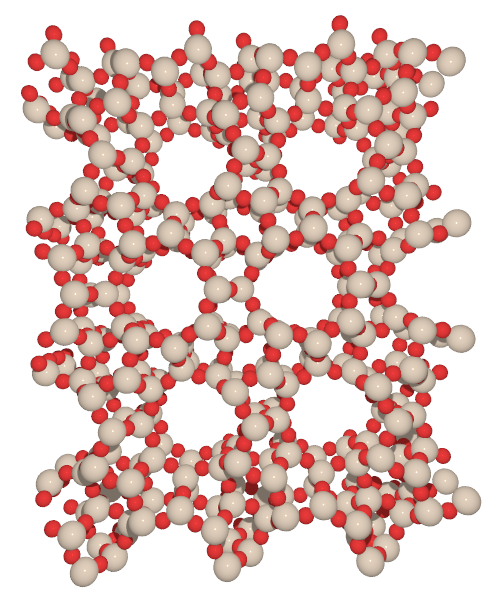
The list of all the zeolite frameworks that are currently available is curated by the International Zeolite Association (IZA) which also makes a catalog with the basic properties of each framework accessible either as the Database of Zeolite Frameworks or in a published form as the Atlas of Zeolite Framework Types available from the IZA publications page.

There are many parameters that can be used to characterize the frameworks and the empty space that can be found inside. Usually the internal voids are categorized as cages and channels with their sizes given as the number of tetrahedrally coordinated atoms (T atoms) forming the ring or units of length suitable for the atomic scale such as Ångstrom.

Here I would just like to mention two of characteristic variables namely the channel size given as the number of T atoms and channel system dimensionality since those two parameters to a large extent determine the applications of a given framework.

The channels present in a given framework are generally classified according to the size of the largest channel into:

small, if the largest channel is assembled with 8 T atoms (and the same number of oxygen atoms),
medium, if the largest channel is assembled with 10 T atoms,
large, if the largest channel is assembled with 12 T atoms,
extra large if the number of T atoms is greater than 12.

The channel system dimensionality on the other hand determines the number of dimensions D that a guest molecule can freely travel through the framework once it enters the pores. Frameworks that have only cages or channels composed of 6 and less T atoms are considered inaccessible and therefore their dimensionality is 0 (D=0). Frameworks with channels composed of more than 6 T atoms and running only in one direction have D=1. In the case of frameworks with multiple channels running in more than one direction the pore dimensionality is dependent on how the channels are mutually connected. If a molecule can move between two channel systems D=2, and when it can move between three channel systems D=3.

By the current count there are 229 unique topologies recognized by IZA. The complete listing of the channel system details for each framework can be found in the Appendix E – Channel System Dimensions of the Atlas of Zeolite Framework Types.

Graphs

Having a convenient way for accessing the data on zeolite frameworks through the zefram package we can explore how certain features are distributed. To perform the basic data analysis and produce the nice visualizations below I chose Bokeh package since it's a very handy tool.

Channel size distribution

Let us start by looking at a histogram below showing the frequencies of the largest channel size (given as the number of T atoms) with a subdivision into different pore system dimensionalities.

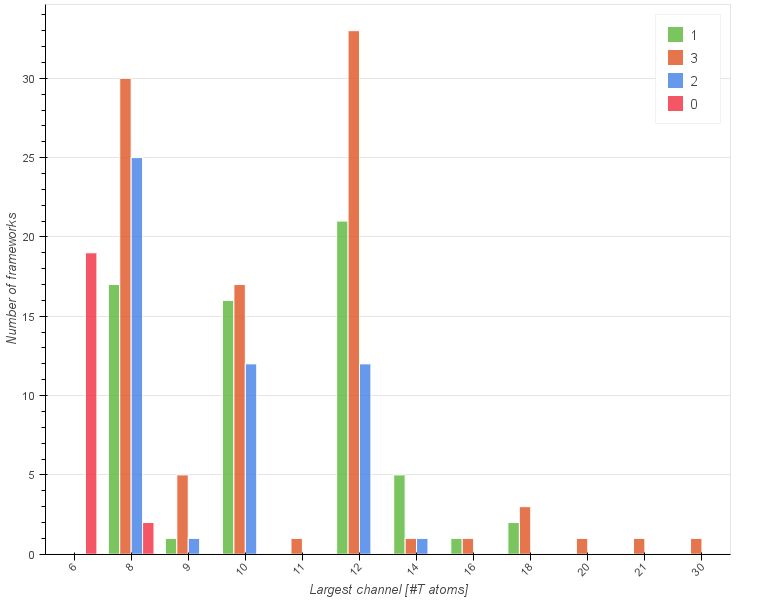
What can be immediately inferred from the graph is that frameworks with even numbered rings dominate over the odd numbered ones. Within the even numbered frameworks there are 74 frameworks with 8 membered ring (MR) channels, 66 with 12 MR and 45 with 10 MR. When it comes to the dimensionality the largest group is composed of three-dimensional frameworks (94), then one-dimensional (63), two-dimensional (51) and zero-dimensional (21).

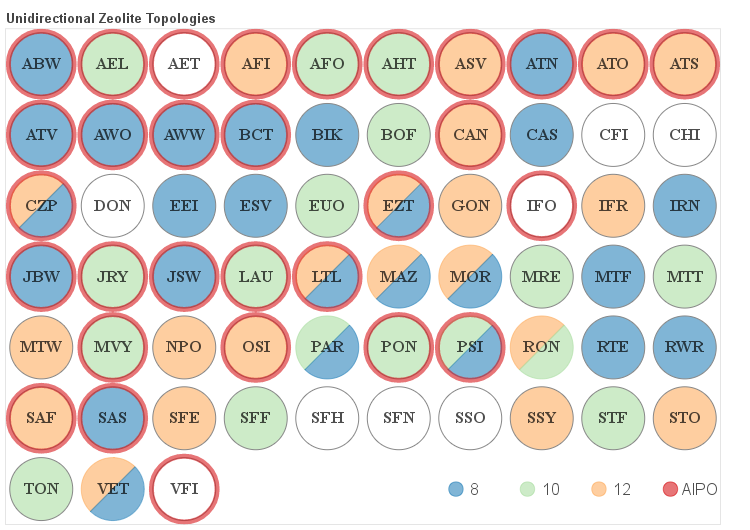
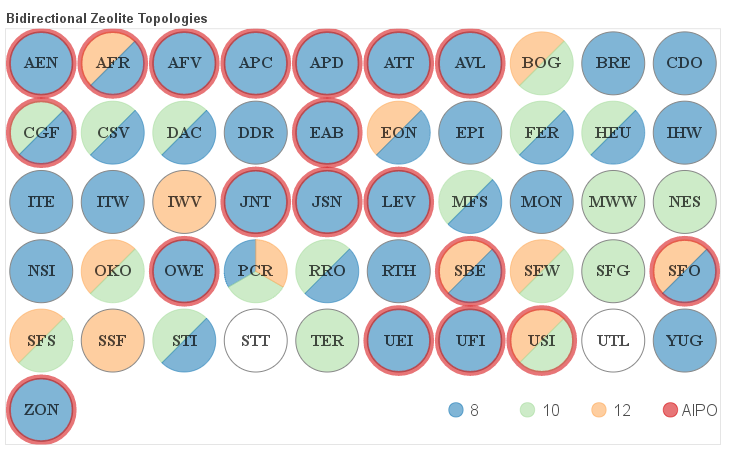
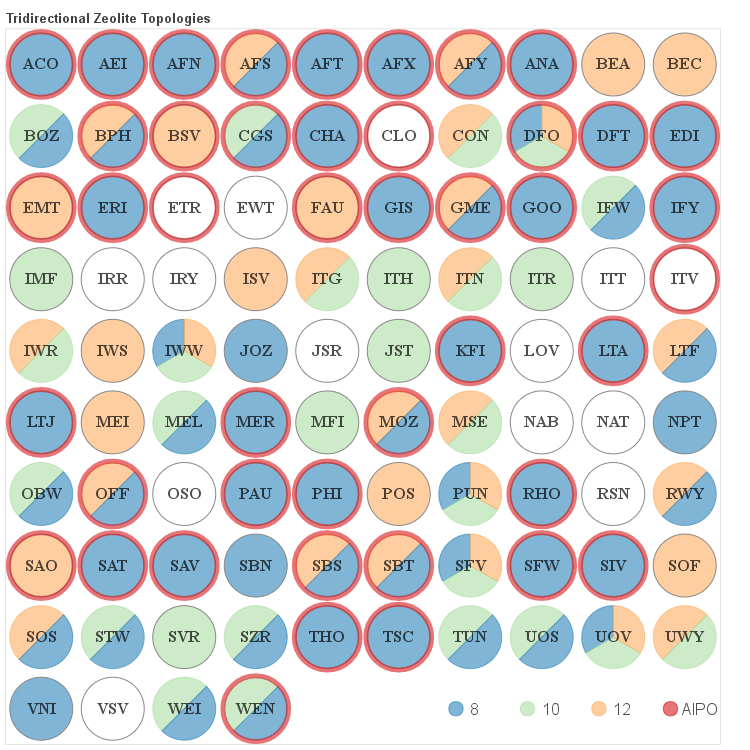
The details about the distribution of different channel sizes for a given pore system dimensionality are visualized in the four figures below. Channels that belong to one of the categories described above as small, medium and large are color coded. Additionally if a given framework is composed solely of even numbered rings it is labeled as AlPO since it would be hypothetically possible to synthesize it as an aluminum phosphate (AlPO).

Zero-dimensional Frameworks

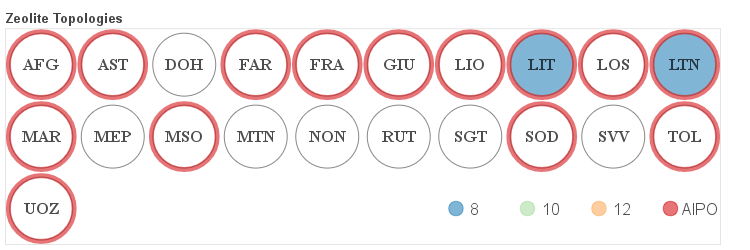
One-dimensional Frameworks

Two-dimensional Frameworks

Three-dimensional Frameworks

If you are interested how to create similar plots to the ones above I uploaded a jupyter notebook that I used the generate the plots to a github repo. There are also additional plots showing some of the other descriptors for the channels and cages size for a given pore system (from ZEOMICS database), such as largest cavity diameter, pore limiting diameter and maximum diameter of a sphere that can be included.